Namu | 나무 개발자 블로그입니다
[방통대] 알고리즘 수업 정리 by namu

목차
- 알고리즘 학습에 앞서서
- 알고리즘의 기초
- 분할정복 알고리즘 1
- 분할정복 알고리즘 2
- 동적 프로그래밍 알고리즘 1
- 동적 프로그래밍 알고리즘 2
- 욕심쟁이 알고리즘 1
- 욕심쟁이 알고리즘 2
들어가며
다음은 2021학년도 1학기 알고리즘 수업에 대한 정리입니다.
1. 알고리즘 학습에 앞서서
컴퓨터 과학에서 알고리즘의 위치
- 컴퓨터 과학 = 컴퓨터 + 데이터 + (프로그램 + 알고리즘)
알고리즘은 컴퓨터 과학 내에서 문제해결을 위한 프로그램을 작성하는 데 사용됩니다. 알고리즘이 없으면 문제 해결 방법을 찾을 수가 없죠.
따라서 컴퓨터 과학은 알고리즘의 과학이라고 할 수 있습니다.
-> “알고리즘과 관련된 이슈를 다루는 학문” (한계, 분석, 개발, 실행, 통신, 표현)
잘 알려진 특정 문제를 통해 알고리즘의 설계 및 분석 방법을 습득해야 하는데,
이를 위해서는 컴퓨터 기반 문제 해결 방법에 대해 체계적으로 생각하는 훈련을 통해
주어진 문제에 대한 지적 추상화 능력 및 통찰력 향상이 이루어져야 합니다.
알고리즘은 왜 필요한가?
컴퓨터 과학은 컴퓨터를 이용해서 주어진 문제를 해결하기 위한 학문입니다. 문제 해결 과정에서는 일련의 절차가 수행되어져야 합니다. 문제 해결을 위한 “레시피”라고 이해하면 편한데, 식재료를 음식으로 만들기까지 단계적인 조리 과정이 문제 해결을 위한 절차와 유사하기 때문입니다. 문제 해결을 위한 일련의 단계적인 처리과정이 곧 알고리즘입니다.
나아가 같은 음식을 만드는 데에도 여러 방식이 존재하는 것처럼 동일한 문제 해결을 위한 알고리즘에도 여러 방식이 있을 수 있습니다. 여러 레시피 중 “맛있고 건강에 도움이 되게 하는” 레시피가 좋은 레시피입니다. 이와 마찬가지로 효율적인 알고리즘이 좋은 알고리즘입니다.
효율적인 알고리즘의 예시 => 퀘닉스버그 다리 문제 ‘한붓 그리기’
- 한 점에서 연결된 선분이 홀수개인 홀수점이 0개 혹은 2개이어야 한다.
- 홀수점이 2개일 경우 홀수점에서 시작해야 한다.
알고리즘의 학습을 위해 필요한 것
- 자료구조
- 프로그램 능력
- 수학적 지식(기반)
본 수업에서는 알고리즘에 활용되는 자료구조 이해와 기본적인 프로그램 능력, 수학적 지식이 필요합니다. 프로그램 능력이라 함은 최소한 코드를 보고 흐름을 이해할 수 있어야 함을 의미하며, 수학적 지식은 논리적인(수학적) 사고가 가능한지가 중요합니다. 자료구조는 복습을 통해 우선적으로 학습하게 됩니다.
2. 알고리즘의 기초
본 강에서는 알고리즘의 개념, 설계, 분석을 공부하고, 성능을 어떻게 평가할 것인지에 대해 살펴봅니다.
학습목표
- 알고리즘의 정의 및 조건 이해
- 알고리즘 설계의 다양성 및 대표적인 설계 기법의 종류를 이해하고 설명할 수 있다
- 알고리즘의 시간 복잡도의 개념을 이해하고 적용할 수 있다
- 점근성능의 표기법의 종류를 이해하고 적용할 수 있다
- 기본적인 점화식의 종류와 개념을 이해하여 설명할 수 있다
알고리즘의 개념
알고리즘은 주어진 문제를 풀기 위한 명령어들의 단계적 나열을 의미합니다.
단, 입출력0개 이상의 input과 1개 이상의 output이 있어야 하며,
명확성각 명령은 모호하지 않고 단순 명확해야 하고,
유한성한정된 수의 단계를 거친 후에는 반드시 종료되어야 하며,
유효성모든 명령은 컴퓨터에서 수행 가능해야 합니다.
위 네 가지 조건이 만족되는 알고리즘이어야만 컴퓨터로 해결할 수 있습니다.
여기서 실용적인 관점 하나를 추가하자면, 알고리즘은 효율적이어야만 합니다.
해결하는데 너무 많은 시간이 소요된다면 그것은 문제해결을 위해 적절한 알고리즘이라고 할 수 없습니다.
알고리즘의 생성 단계
설계 -> 표현/기술 -> 정확성 검증 -> 효율성 분석
…
시간 복잡도
시간 복잡도는 주어진 알고리즘의 연산 횟수를 함수화하여 그 중 최고차항에 대한 Big-oh(빅-오) 표기법으로 나타냅니다.
점근성능, 표기법
성능을 측정할 때는 입력 크기 n이 무한대로 커짐을 가정합니다. 이에 따라 상수 및 최고차항보다 작은 차수의 항들은 사실상 의미가 없어집니다. 알고리즘의 다항식 함수에서 최고차항만을 취해서 표현하는 것을 점근성능이라고 합니다.
점근성능은 정확한 값이 아닌 어림값입니다. 하지만 입력 크기에 따른 증가추세를 파악하여 알고리즘 간 우열을 표현하는 데는 아주 용이합니다.
- [정의] Big-oh 점근적 상한
어떤 양의 상수 c와 n0이 존재하여 모든 n>=n0에 대하여 f(n)<=c*g(n)이면 f(n)=O(g(n))이다.
Big-oh 점근적 상한 정의가 의미하는 바는 내가 정의한 알고리즘 함수 f(n)의 수행시간의 상한식 g(n)입니다. 즉 아무리 성능이 나빠져도(수행시간이 늘어나도↑) 상한함수보다는 나빠지지(수행시간이 늘어나지↑) 않음을 의미합니다. 내 알고리즘의 최악의 수행사례를 가정하여 시간 복잡도를 표현하는 것입니다. 이를 O(g(n))으로 표기합니다.
- [정의] Big-omega 점근적 하한
어떤 양의 상수 c와 n0이 존재하여 모든 n>=n0에 대하여 f(n)>=c*g(n)이면 f(n)=Ω(g(n))이다.
Big-omega 점근적 하한은 Big-oh와는 반대로 하한식 g(n)을 표현합니다. 이는 내 알고리즘의 성능이 아무리 좋아져도(수행시간이 줄어들어도↓) 하한함수보다는 좋아지지(수행시간이 줄어들지↓) 않음을 의미합니다.
- [정의] Big-theta 점근적 상하한
어떤 양의 상수 c1, c2와 n0이 존재하여 모든 n>=n0에 대하여 c1g(n)<=f(n)<=c2g(n)이면 f(n)=θ(g(n))이다.
추가적으로 Big-theta 점근적 하한은 상한식과 하한식을 전부 포함하는 g(n)을 표현합니다.
일반적으로 시간 복잡도를 표현할 때는 Big-oh 점근적 상한식을 활용하므로, O(상수를 제거한 상한식의 최고차항)으로 나타냅니다.
ex) f(n) = 3n² + 5 => O(n²)
주요 O-표기 간의 연산 시간의 크기 관계
O(n), O(n^2), O(n^3)중 어느 것이 가장 효율적인(연산횟수 ↓) 알고리즘일까요? 단순히 n에 수를 늘려가며 대입하여 비교해봐도 O(n)의 연산 횟수 증가정도가 가장 작습니다.
주요 알고리즘 함수식 비교
- O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(2ⁿ) < O(n!)
오른쪽으로 갈수록 연산 횟수 정도가 더 큰 비효율적(연산횟수, 수행시간 ↑) 알고리즘입니다.
 이미지 출처: velog.io/@raram2
이미지 출처: velog.io/@raram2
실용적으로 구해보기
알고리즘의 함수식을 구한 후 최고차항 함수식 g(n)을 추출하여 빅-오로 표기하는 것이 정석적인 방법이나, 실용적으로는 알고리즘 내에 나타난 루프의 반복 횟수를 조사하여 시간 복잡도를 취합니다.
설명하자면 n이 무한대로 증가함에 따라 가장 영향을 받는 부분이 반복문이기 때문에 위와 같이 합니다. 알고리즘의 함수식에서 반복 상황이 중첩적으로 가장 많은 루프를 최고차항으로 판단합니다. 그 외 최고차항에 붙은 상수는 반복문 내 존재하는 단순 연산들의 개수를, 낮은 차수들은 중첩 반복이 더 적은 또다른 반복문을, 기타 상수는 함수 내 추가적인 연산만을 의미하기 때문에 점근 상황에서는 무시 가능합니다.
순환 알고리즘의 성능
순환 알고리즘의 시간 복잡도는 일반적인 방법으로 알아내기 어렵습니다. 따라서 각 순환 알고리즘에 따른 점화식을 활용합니다. 대표적인 순환 알고리즘인 재귀식을 활용하는 이진 탐색의 점화식은 다음과 같습니다.
- 재귀(recursion)
- T(n) = T(n/2) + O(1), T(1) = c1
매번 점화식을 풀기보다는 아래 기본 점화식과 폐쇄형을 미리 숙지해 둡시다.
 이미지 출처: atoz-develop.tistory.com
이미지 출처: atoz-develop.tistory.com
3. 분할정복 알고리즘 1
이번 강의에서는 분할정복의 원리, 특징, 처리 단계 등을 파악하고 이를 응용하여 이진 탐색, 퀵 정렬을 살펴봅니다.
3.1 분할정복 방법의 원리
순환적으로recursively 문제를 푸는 하향식top-down 접근 방법
주어진 문제를 더 이상 나눌 수 없을 때까지 순환적으로 분할하고, 분할된 작은 문제들을 해결한 후 각각의 해를 결합하여 본래의 해를 구하는 방식입니다.
여기서 주목할 특징은, 분할된 작은 문제는 원래의 문제와 동일하다는 사실입니다. 단지 입력 크기만 작아질 뿐입니다.
그리고 분할된 작은 문제는 서로 독립적이기 때문에, 모든 분할 결과를 통합하여 원래의 해를 구할 수 있습니다.
분할 정복의 처리 단계는 다음과 같습니다.
- 분할정복 처리 단계
- 분할: 주어진 문제를 여러 개의 작은 문제로 분할
- 정복: 더 이상 나눌 수 없을 때까지 순환적으로 분할하여 작은 문제의 해 구하기
- 결합: 작은 문제로 정복된 해를 결합하여 원래 문제의 해 구하기
문제에 따라 마지막 결합 단계가 생략될 수 있습니다.
- 분할 정복이 적용된 알고리즘 비교
- 이진 탐색: 탐색 범주를 절반씩 줄여나가며 해를 도출(결합 단계x)
- 합병 정렬: 범주를 절반씩 줄여 원자화된 해를 구한 뒤 병합
- 퀵 정렬: 분할하되, 피벗에 따라 분할 비율이 달라지며 정렬
- 선택 정렬: 서로 다른 비율로 분할하되, 정렬의 범주를 선택된 어느 한쪽으로 좁혀나감
3.2 이진 탐색
이진 탐색의 조건은 입력 데이터가 정렬되어 있어야 합니다. 그래야 범주를 절반씩 좁혀나가며 탐색할 수 있습니다.
이진 탐색 알고리즘의 특징
- 데이터가 정렬된 경우만 적용 가능!
- insert/delete 연산은 이후 데이터의 이동을 수반(평균 n/2개의 데이터 이동)
- 따라서 삽입과 삭제가 빈번한 응용에서는 부적합!
입력된 리스트 A에서 탐색키 x의 인덱스를 반환하는 과정은 다음과 같습니다.
(1) 기본적으로 중앙값 A[mid] 값을 선정하여 x와 비교하는 방식으로 분할 정복합니다. (mid는 가운데 인덱스)
(2) x == A[mid], 탐색 성공이므로 mid 반환
(3) x < A[mid], 중앙값 기준 왼쪽 부분 리스트에 대해 (1)의 과정 순환 호출
(4) x > A[mid], 중앙값 기준 오른쪽 부분 리스트에 대해 (1)의 과정 순환 호출
정렬된 리스트를 이렇게 분할해 나아가다 보면 마지막에 단일 원소만 남게 되는데, 이것마저 찾고자 하는 x 값과 다르다면 -1 등 지정된 False 값을 반환하도록 합니다.
위 과정을 분할정복 처리 단계로 살펴보면, (1)~(2) 과정을 통해 분할하고 (3)~(4) 과정을 순환반복하며 정복하게 됩니다. 원하는 값의 인덱스를 탐색하는 과정이므로 결합 과정은 생략됩니다.
이진 탐색에서 주목할 부분은 탐색을 반복할 때마다 대상 원소의 개수가 1/2씩 감소한다는 사실입니다.
이제 파이썬을 활용하여 코드로 구현해 보겠습니다.
def binary_search(nums, left, right, x):
if left > right:
return -1 # 잘못된 인덱스 지정 혹은 더이상 찾지 못할 경우
mid = (left + right) // 2 # 분할, (1)번 과정
if x == nums[mid]: # 분할, (2)번 과정
return mid
elif x < nums[mid]: # 정복, (3)번 과정
return binary_search(nums, left, mid - 1, x)
else: # x > nums[mid], 정복, (4)번 과정
return binary_search(nums, mid + 1, right, x)
앞서 설명한 대로 1/2씩 분할하며 탐색을 수행하되, 원하는 값을 찾을 때까지 재귀적으로 정복해갑니다.
다만, 재귀적인 호출 방식은 사람이 보기에 편하나 컴퓨터 입장에서는 함수 호출 스택이 중첩되므로 효율성이나 메모리 면에서 좋지많은 않습니다. 이진 탐색 알고리즘의 경우는 mid 인덱스를 단순히 바꿔가는 반복문으로 재귀호출을 대체할 수 있습니다.
import math
def binary_search_loop(nums, x):
if not nums:
return -1
left, right = 0, len(nums) - 1
while left <= right:
mid = math.floor((left + right) / 2)
if x == nums[mid]:
return mid
elif x < nums[mid]:
right = mid - 1
else:
left = mid + 1
return -1
최대 분할 횟수와 최대 비교 횟수는?
이진 탐색은 중앙값을 선택해 탐색 범주를 절반씩 줄여나간다고 했습니다.
그렇다면 입력 크기 n일 때 최대 분할 쵯수와 최대 비교 횟수는 어떻게 알수 있을까요?
- 최대 분할 횟수
- 1회 n/2만큼 분할합니다.
- 2회 n/2^2만큼 분할합니다.
- …
- k회 분할 시 n/2^k만큼 분할합니다.
- 따라서 최대 분할 횟수 k = floor(logn) 입니다.
- 최대 비교 횟수
- 최대 분할 횟수 k마다 비교하고,
- 최초 분할시에 한번 비교하고 로직을 수행하므로,
- 최대 분할 횟수 k + 1회입니다.
이제 이진 탐색 알고리즘의 성능을 분석해 봅시다.
입력 크기 n에 대한 모든 비교 횟수의 합을 T(n)이라 했을 때, 순환 호출에서의 비교 횟수에 순환 바깥에서 고정적인 비교 횟수를 더해 점근성능을 도출합니다.
여기서 고정적인 비교 횟수는 곧 상수(O(1))이고, 순환 호출은 범주 n이 절반씩 줄어들며(n/2) 진행됩니다. 따라서,
이진 탐색 알고리즘의 성능
T(n) = T(n/2) + O(1) (n>1), T(1) = 1 T(n) = O(logn)
3.3 퀵 정렬
퀵 정렬은 피벗 원소를 선정하여 left, right 의 대소관계를 비교하는 정렬 알고리즘입니다.
- 퀵 정렬의 분할정복 처리 단계
- 분할: 리스트를 pivot을 중심으로 좌우 분할
- 정복: 작은 수는 왼쪽, 큰 수는 오른쪽에 위치하도록 재배치하는 동일한 퀵 정렬 로직을 분할 부분들에 대해 순환적으로 반복적용
- 결합: 정복이 완료되면 리스트는 정렬되기 때문에 결합은 필요 없음
분할 정복으로써의 퀵 정렬에서 주목할 부분은 피벗pivot과 파티션partition 함수입니다. pivot은 주어진 리스트의 첫 번째 값 혹은 (통상적으로) 중간값을 선정하게 되며, partition 함수는 분할 함수로써 pivot을 활용해 좌우 범주를 분할하여 정렬을 수행합니다.
partition 함수의 슈도 코드는 다음과 같습니다.
int partition(A[], n) { // A는 제공된 정수 리스트, n은 리스트의 길이
/*
* pivot을 리스트의 첫 번째 원소로 선택할 것이므로,
* Left는 1번 인덱스, Right는 범주내 마지막 원소인 n - 1번 인덱스
*/
Left = 1; Right = n - 1;
pivot = A[0]; // 첫 번째 원소 선택
while (Left < Right) {
while (Left < n && A[Left] < pivot) Left++; // pivot 기준으로 더 큰 Left 원소 검색
while (Right > 0 && A[Right] >= pivot) Right--; // pivot 기준으로 더 작은 Right 원소 검색
if (Left < Right) {
// 선택된 Left, Right 원소 교환
temp = A[Left];
A[Left] = A[Right];
A[Right] = temp;
} else {
// pivot 기준을 지나쳤으므로 마무리. 분할 기준 위치로 pivot 이동
// 설명하자면, 실제 리스트 상 첫 벗째 위치에 있던 pivot 원소가
// 분할 정렬 완료 후 제 자리로 찾아가도록 하는 과정
temp = A[0];
A[0] = A[Right];
A[Right] = temp;
}
}
// pivot이 위치하는 원소의 인덱스 반환
// 이것을 기준으로 좌우 분할들에 대한 다음 분할정복 로직이 수행됨
return Right;
}
슈도 코드에서는 pivot을 리스트의 첫 번째 원소로 선택했지만, 이미 정렬된 리스트가 입력되었을 때 이것은 최악의 수행 시간을 나타내게 됩니다.
왜냐하면 분할할 때마다 왼쪽 부분리스트의 길이는 0, 오른쪽 부분리스트의 길이는 입력 크기 n - 1 로 나눠지게 되어(정렬되었으므로), 결국 리스트의 모든 요소를 탐색하는 결과가 나타나기 때문입니다. 마지막 요소를 pivot 삼아도 마찬가지입니다. 이는 O(n)의 시간 복잡도에 비례합니다. 이와 반대로 최선의 경우라면 1/2씩 이상적으로 분할해 나가는 O(logn)에 비례합니다.

- 극심한 불균형적 분할
- (1) 입력 데이터로 정렬된 리스트가 투입되고,
- (2) pivot이 항상 부분리스트의 최소값 또는 최대값으로 선정
- 0:n-1, n-1:0 -> pivot만 제자리를 잡고 나머지 모든 원소가 하나의 부분리스트가 되는 경우
T(n) = T(n-1) + T(0) + O(n) (n>0), T(0)=0 T(n) = T(n-1) + O(n) T(n) = O(n^2)
- 0:n-1, n-1:0 -> pivot만 제자리를 잡고 나머지 모든 원소가 하나의 부분리스트가 되는 경우
가장 극심한 불균형적 분할 형태에서는 모든 원소를 pivot 삼게 되므로 분할 정복 과정에서 n에 비례하는 O(n) 반복 수행시간이 걸리고, 각 반복마다 partition이 분할하는 데 걸리는 고정적인 시간 O(n)이 수행되므로 총 시간복잡도는 O(n^2)입니다.
- 가장 균형적인 분할
- 리스트가 pivot을 중심으로 항상 동일한 크기의 두 부분배열로 분할되는 경우 -> n/2:n/2 비율로 분할
- 이때 pivot은 항상 중간값이 됨
T(n) = T(floor(n/2)) + T(floor(n/2)) + O(n) (n>1), T(1)=1 T(n) = 2T(n/2) + O(n) T(n) = O(nlogn)
반대로 가장 이상적인 형태에서는 pivot 선택이 매번 중간값이 되어 분할의 범주가 절반씩 줄어들게 되므로 O(logn)의 더 나은 수행시간이 걸립니다. 각 반복마다 partition O(n)의 분할이 시행되므로 총 시간복잡도는 O(nlogn)입니다.
평균의 수행시간을 구한다고 할 때도 결국 pivot은 중간값으로 수렴되므로 O(nlogn)의 시간복잡도가 도출됩니다.
그렇다면, 우리가 실제로 퀵 정렬을 코드로 구현할 때 어떻게 하면 O(nlogn)의 성능이 보장되도록 할수 있을까요? 앞서 극심한 불균형적 분할의 조건을 만족시키지 않으면 되겠죠.(-> 정렬된 리스트 and 첫 번째 혹은 마지막 요소 선택)
입력으로 정렬된 리스트가 들어오는 것은 프로그래머의 통제 밖의 이야기이므로, 그런 최악의 경우를 가정했을 때 pivot 선택의 임의성을 보장해주면 위 조건을 만족시키지 않을 수 있습니다.
그래서 통상적으로 리스트의 첫 번째 요소가 아닌 중간 요소를 pivot으로 선택하도록 구현합니다. 다음은 pivot을 중간값으로 선정하는 python 구현입니다.
from math import floor
def partition(nums, left, right):
pivot = nums[floor((left + right) / 2)]
while left <= right:
while left < len(nums) and nums[left] < pivot: left += 1
while right >= 0 and nums[right] > pivot: right -= 1
if left <= right:
nums[left], nums[right] = nums[right], nums[left]
left += 1
right -= 1
return left
def quick_sort(nums, left, right):
if left < right:
pivot = partition(nums, left, right)
quick_sort(nums, left, pivot - 1)
quick_sort(nums, pivot, right)
return nums
quick_sort() 함수에서는 pivot에 따라 분할하여 정복을 반복하며, partition() 함수에서 pivot은 매번 리스트 범주의 중간값을 선정하도록 구현되었습니다.
4. 분할정복 알고리즘 2
분할정복 알고리즘은 분할, 정복, 결합의 세 단계로 진행된다고 하였습니다. 이번 강의에서는 분할정복 방법이 적용된 분할 정렬과 선택 문제에 대해서 다룹니다.
4.1 합병 정렬
4.2 선택 문제
5. 동적 프로그래밍 알고리즘 1
본 강의를 통해 동적 프로그래밍 방법과 원리를 이해하고, 피보나치 수열과 연쇄 행렬 곱셈 알고리즘을 다뤄보기로 합니다.
동적 프로그래밍 방법의 원리
- 소문제의 해를 메모이제이션하여 보다 큰 크기의 문제의 해를 점진적으로 만들어가는 상향식bottom-up 방법
- 소문제는 입력의 크기만 작지 원래의 문제와 해결 방법은 동일 > 점화식 도출 가능
- 일반적으로 최대값이나 최소값을 구하는 최적화 문제에서 많이 활용됨
최적성의 원리principle of optimality 를 만족하는가?
소문제의 해가 모여 본래의 해가 도출되는가?
동적 프로그래밍의 적용 과정은 다음과 같습니다.
동적 프로그래밍은 먼저 1.최적성의 원리가 성립하는지 확인하고, 2.점화식을 도출하여 3.가장 작은 소문제의 해로부터 시작해 점차 더 큰 문제의 해를 구해나갑니다.
피보나치 수열
이것은 앞선 두 수의 합이 자기 자신이 되는 원리를 갖는 수열입니다.
이 원리가 곧 최적성의 원리를 만족하게 되며, 점화식은 f(n) = f(n - 2) + f(n - 1) 입니다.
피보나치 수열을 파이썬으로 구현하면 다음과 같습니다.
def fibonacci(n: int):
memoization = [0, 1]
for i in range(2, n + 1):
memoization.append(memoization[i - 2] + memoization[i - 1])
return memoization
점화식을 그대로 구현하여 가장 작은 소문제인 0과 1로부터 상향식으로 최종 결과를 도출했습니다. 이것의 반복 로직의 횟수는 입력된 수 n 의 크기에 정비례하므로 시간복잡도 O(n) 입니다.
그런데 동일한 로직을 분할 정복 방법으로 풀어 봅시다. 분할 정복은 결과값으로부터 역순으로 찾아가는 하향식top-down입니다.
def fibonacci(n: int):
if n <= 1:
return n
return fibonacci(n - 2) + fibonacci(n - 1)
여기서는 fibonacci 함수 자신을 재귀적으로 호출하는 순환 형태를 띕니다. 이것도 입력된 수 n 의 크기에 동일하게 비례하는 것처럼 보이지만, 상향식 방법에 비해 숨겨진 차이점이 있습니다.
그것은 중간에 반복되는 동일 연산이 존재한다는 것입니다.
예를 들어, f(5) 는 f(3) + f(4) 이고, f(4) 는 f(2) + f(3) 의 결과이므로
이것만 놓고 보아도 f(3) 이 두 번 중복 계산됩니다.
메모이제이션은 소문제를 한 번만 계산하고 필요할 때 조회해서 사용할 뿐이므로 중복 계산이 존재하지 않습니다. 따라서 피보나치 수열의 구현에 있어서 하향식 방법보다는 상향식 방법이 더 효율적입니다.
연쇄 행렬 곱셈
먼저 행렬의 곱셉이 어떤식으로 이루어지는지 살펴봅시다.
행렬의 곱셈에서는 결합법칙이 성립됩니다. 결합법칙이 이루어지기 위해서는 곱셈을 수행하는 인접한 두 행렬의 열과 행의 개수가 일치해야 합니다. 따라서,
(3 x 2) 행렬과 (2 x 4) 행렬의 곱셈 결과는 (3 x 4) 형태입니다.
만약에 전자의 열 개수와 후자의 행 개수가 일치하지 않는다면 행렬의 곱셈은 불가능합니다.
그렇다면 여러 개의 행렬을 연쇄적으로 곱하는 경우에는 어떻게 될까요? 결합법칙에 따라,
(3 x 2) * (2 x 4) * (4 x 1) 의 결과는 (3 x 1) 형태가 됩니다.
여기서 주목할 점은 결과가 나오기까지 두 가지 결합의 경우의 수가 발생한다는 것입니다.
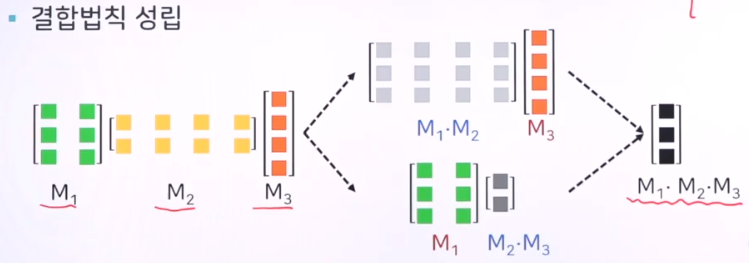
경우의 수 첫 번째는 앞선 두 개를 결합하고 나머지 하나를 결합하는 것이고, 다른 경우의 수는 그 반대로 하는 것입니다.
나아가 연쇄 행렬의 개수가 많아지면 경우의 수도 더 많아질 것입니다.
이제 동적 프로그래밍으로써의 요건이 나타나기 시작합니다. 연쇄 행렬 곱셈에서 우리의 목적은 가장 효율적인 연쇄 곱셈 경우의 수를 찾는 것입니다.
연쇄 행렬 곱셈 문제?
n 개의 행렬을 연쇄적으로 곱할 때 최적의 곱셈 순서를 구하는 문제
최대값 혹은 최소값을 구할 때 사용되는 DP 의 조건을 만족하게 됩니다. 그렇다면 최적성의 원리를 만족할까요?
물론입니다. 앞선 차례에서 행렬들의 곱셈의 결과(소문제)를 다음 차례에서 사용하게 되므로 최적성의 원리를 만족합니다.
최적성의 원리를 만족하는가?
n 개 행렬를 곱할 때 최적의 순서는 n-1 개 행렬을 곱할 때 최적의 순서로부터 도출되므로 만족.
이는 소문제가 최적의 순서가 아니라면 그것을 포함한 더 큰 문제의 최적의 순서는 성립될 수 없음을 의미합니다.
6. 동적 프로그래밍 알고리즘 2
최적 부분 구조(Optimal Substructure)와 중복되는 부분 문제(Overlapping Subproblem)의 특징을 갖는 동적 프로그래밍에서는 memoization을 빈번하게 사용합니다. 가능하다면 반복문으로 구현하고 보텀업 방식을 찾아가는 것이 성능상 좋습니다.
스트링 편집 거리 문제 (Edit distance)
이 문제는 문자열 Xi를 문자열 Yj로 편집하는 데 드는 최소비용 구하기입니다.(i, j는 각 문자열의 길이입니다.) 편집에는 삽입I, 삭제D, 변경C 연산이 있는데 각각의 비용이 소요됩니다. 특정 순서 i의 문자를 편집하고자 할 때 Xi 문자를 삭제할지 새로 삽입할지, 아니면 Xi를 변경할지 결정하되, 최소 비용이 드는 것을 선택해야 합니다.
따라서 두 문자열 사이의 편집 거리는 이들의 부분 문자열 사이의 편집거리를 포괄하게 되어 최적성의 원리를 만족합니다. 즉, X 문자열 중 특정 위치의 문자까지의 편집 최소비용은 그 이전 문자까지의 편집 최소비용을 포함한다는 의미입니다. 따라서 동적 프로그래밍 방법을 적용할 수 있습니다.
직전 부분 문자까지의 최소 편집 거리를 통해서 마지막 문자까지의 최소 편집 거리를 도출하는 방식이므로, 그 상황은 (1)마지막 문자열을 삭제하는 경우, (2)마지막 문자열을 삽입하는 경우, (3)마지막 문자열이 같거나 같도록 만들어주는 경우의 총 세 가지가 있으며, 이 중 최소값을 구하면 됩니다. 이에 따른 점화식은 다음과 같이 도출합니다.
E(i, j) = min[E(i - 1, j) + δD,
E(i, j - 1) + δI,
E(i - 1, j - 1) + (0 / δC)]
* 0 / δC = 0, xi = yi or 0 / δC, xi != yi
최소값 E(i, j)를 구하되(min), 이전 단계로부터 문자를 삭제하거나 삽입하거나 같게 하는 경우 중 하나가 선택되도록 하는 것입니다.
DP는 메모이제이션을 많이 활용한다고 했으므로, 부분 구조들의 최소비용 저장을 위해 문자열 X, Y에 해당하는 이차원 배열을 만들어 직전 부분 구조로부터 해당 순서의 최소비용을 구해나갈 수 있습니다. 예제 문제를 봅시다.
예제 1) X = bbabb, Y = abaa, δD = δI = 1, δC = 2 일때 edit distance 구하기
| a | b | a | a | ||
| 0 | 1 | 2 | 3 | 4 | |
| b | 1 | 2 | 1 | 2 | 3 |
| b | 2 | 3 | 2 | 3 | … |
| a | 3 | ||||
| b | 4 | ||||
| b | 5 | E(i, j) |
/* (1, 1)의 최소비용 구하기 */
E(1, 1) = min[E(0, 1) + 1, E(1, 0) + 1, E(0, 0) + 2]
= min[2, 2, 2] = 2
/* (1, 2)의 최소비용 구하기, 같은 문자이므로 변경(δC)시 비용은 0 */
E(1, 2) = min[E(0, 2) + 1, E(1, 1) + 1, E(0, 1) + 0]
= min[3, 3, 1] = 1
/* (1, 3)의 최소비용 구하기 */
E(1, 3) = min[E(0, 3) + 1, E(1, 2) + 1, E(0, 2) + 2]
= min[4, 2, 4] = 2
...
순서대로 각 항목의 최소비용을 구해나가는 과정을 메모이제이션으로 나타낸 것입니다. 최적 부분 구조가 보이시나요? 각 순서의 항목들은 이전 문자까지의 최소비용으로부터 구해집니다. 삭제, 삽입 시 1의 비용이 추가되고 변경시 2의 비용이 순서대로 추가되는 것이죠. 만약 Xi -> Yj 문자가 같다면 바꿀 필요가 없으므로 변경 비용은 0일 것입니다.
이런 식으로 E(i, j)를 구하게 되면 최소 비용은 5가 도출됩니다. 이번에는 의미 있는 문자열로 문제를 풀어봅시다.
예제 2) X = SNOWY, Y = SUNNY, δD = δI = 1, δC = 2 일때 edit distance 구하기
| S | U | N | N | Y | ||
| 0 | 1 | 2 | 3 | 4 | 5 | |
| S | 1 | 0 | 1 | 2 | 3 | 4 |
| N | 2 | 1 | 2 | 1 | 2 | 3 |
| O | 3 | 2 | 3 | … | ||
| W | 4 | |||||
| Y | 5 | 4 |
/* (1, 1)의 최소비용 구하기, 같은 문자이므로 변경(δC)시 비용은 0 */
E(1, 1) = min[E(0, 1) + 1, E(1, 0) + 1, E(0, 0) + 0]
= min[2, 2, 0] = 0
/* (1, 2)의 최소비용 구하기 */
E(1, 2) = min[E(0, 2) + 1, E(1, 1) + 1, E(0, 1) + 2]
= min[3, 1, 3] = 1
/* (1, 3)의 최소비용 구하기 */
E(1, 3) = min[E(0, 3) + 1, E(1, 2) + 1, E(0, 2) + 2]
= min[4, 2, 4] = 2
...
풀이 과정은 위와 동일합니다. 직전 문자의 최소비용으로부터 다음 문자의 최소비용을 도출하는 방식입니다.
이제 코드로 구현을 해볼텐데, 위 알고리즘의 순서대로 하면 됩니다.
- 입력: X, Y 문자열과 각 편집비용 입력
- 충분한 크기의 메모이제이션 생성(X, Y 문자열 길이의 +1)
- 초기화: 초기값 세팅
- 초기값은 (1, 0), (2, 0), …, (i, 0) 자리에 X의 각 문자를 세팅하고, Y 문자열에 대해서도 동일하게 하면 됩니다.
- 탐색: i, j 순서까지 반복하여 최소비용 구하기
- 메모이제이션 이차원 배열의 각 항목에 최소비용을 넣되,
- 각각의 직전 항목으로부터 insert, delete, change 중 최소비용을 선택합니다.
- 최소비용 반환
이것을 파이썬으로 구현해 보겠습니다.
def solution(str1, str2, insert, delete, change): # 1.
n, m = len(str1), len(str2)
# 2. Make memoization
answer = [[0 for _ in range(m + 1)] for _ in range(n + 1)]
# 3. Initialize values
for i in range(1, n + 1):
answer[i][0] = i * insert
for j in range(1, m + 1):
answer[0][j] = j * insert
# 4. Calc distance
for i in range(n):
for j in range(m):
answer[i + 1][j + 1] = min(
answer[i][j + 1] + delete,
answer[i + 1][j] + insert,
answer[i][j] + (0 if str1[i] == str2[j] else change),
)
return answer[n][m]
solution() 함수는 1. 문자열 두 개를 입력받아 이전 문자열에서 나중 문자열로 편집하는 최소비용을 반환합니다.
insert, delete, change 의 연산별 비용은 함수 내에 고정적으로 세팅할 수 있습니다.
다음으로 2. 메모이제이션을 생성하되, 초기비용 0으로부터 출발하기 위해 각 문자열의 길이 +1에 해당하는 이차원 배열을 만듭니다.
그리고 3. 초기값 세팅 시 (x축, 0), (0, y축) 방향으로 insert 비용만큼 값이 증가하도록 넣습니다.
insert = 1 이라면 1씩 증가할 것이고, 2라면 x2씩 값이 증가할 것입니다.
마지막으로 최적 부분 구조가 되는 4. 각 문자별 최소비용을 상향식으로 계산해 나갑니다.
여기서 추가적으로 어떤 방식으로 변경되는지 편집 방향을 알고 싶다면, 마지막 최소비용이 구해지는 E(n, m)으로부터 역추적하는 로직 P를 추가합니다.
플로이드(Floyd) 알고리즘 - 모든 정점 간의 최단경로(Shortest Path) 구하기
가중 방향 그래프에서 최단 경로를 구하는 방법은 여러 가지가 있습니다. 그 중 플로이드 알고리즘은 모든 정점 간의 최단 경로를 다이나믹 프로그래밍 방식으로 구해나가는 것입니다. 즉, 최적 부분 구조를 갖는다는 의미이죠.
이와 다르게 단일 출발점으로부터 다른 모든 정점까지의 최단 경로를 구하는 방법을 다익스트라Dijkstra 알고리즘이라고 합니다. 이것은 기본적으로 그리디greedy, 탐욕 알고리즘으로 분류되지만, 이전 방문노드의 값을 활용하므로 최적 부분 구조로 볼 수도 있습니다.
어쨌든 플로이드의 아이디어는 이렇습니다. 모든 정점 간의 최단경로를 구하기 위해 최적 부분 구조의 특성을 이용하여 모든 정점 간의 관계가 표현된 이차원 배열 메모이제이션에 상향식으로 최소 가중치 비용을 채워 나갑니다. 특정 정점 i, j를 의미하는 각 항목에서의 최소비용을 구할 때 경유하는 정점 k를 순차적으로 늘려나가며 최소비용을 찾습니다. 두 정점 간에 직접 연결이 최소비용이기도 하지만, 특정 정점을 경유할 시 그것이 최소비용이 될 수도 있습니다. 또는 직접연결이 불가하여 비용을 구하지 못하던 정점들도, 여러 다른 정점들을 경유할 시 최소비용이 도출될 수 있습니다.
다시 말하자면, 두 정점 i와 j 간의 최단경로를 구할 시 경유하는 정점 1부터 k 까지를 모두 고려하여 그 중 최소비용을 사용합니다. 정점 k 를 경유하는 시점의 최단경로는 정점 k - 1 까지 경유하는 최소비용을 최적 부분으로 갖는다는 점을 생각하십시오. 정점 k - 1 입장에서는 현재까지가 최단거리일 것이고, 정점 k 까지 고려하는 상황에서는 k 를 경유하는 시점의 거리를 이전 최단거리와 비교해야 할 것입니다. 정점 k 를 고려하기 위해서는 (출발점인 i부터 k 까지의 최단거리 + k부터 목적지 j 까지의 최단거리) 계산을 하면 됩니다. 그럼 플로이드의 점화식을 살펴봅시다.
D(i, j, 0) = d(ij) = w(ij), 1 <= i, j <= n /* 경유 정점이 없는 경우 가중치를 그대로 사용 */
D(i, j, k) = min[ D(i, j, k - 1), D(i, k, k - 1) + D(k, j, k - 1) ]
최단거리 D(i, j, k)에서 k 는 경유지점, i와 j는 각각 출발지점과 목적지점을 의미합니다. 뒤에 min 연산에서는 ij 까지 중 k - 1을 경유하는 상황의 최단거리와, k를 경유하는 최단거리 중 작은 것을 선택합니다.
알고리즘 구현 시, 순서는 다음과 같이 하면 됩니다.
- 입력: 모든 정점과 가중치 값 입력
- 초기화: 입력값에 따라 이차원 배열(인접 행렬)로 비용 초기화
- 이 때 ij로 직접 연결을 고려하므로, 직접 연결 간선이 존재하는 경우 그것의 가중치로,
- 존재하지 않는 경우 무한대의 값으로 초기화합니다.
- 탐색: 경유 노드를 기준으로 모든 출발점과 끝점간 반복하며 최소비용을 구합니다.
이것을 파이썬으로 구현해 보겠습니다.
import sys
INF = sys.maxsize # Static Infinite value
def solution(n, graph, start, end):
# 2. Make memoization and Initialize values
answer = [[INF]*n for _ in range(n)]
for i in range(n):
for j in range(n):
answer[i][j] = graph[i][j]
# 3. Calc distance -> 경유하는 k기준
for k in range(n):
for i in range(n):
for j in range(n):
if answer[i][j] > answer[i][k] + answer[k][j]:
answer[i][j] = answer[i][k] + answer[k][j]
return answer[start - 1][end - 1] # Start with index 0
구현 자체는 상당히 쉽습니다. 가중 방향 그래프에 맞게 초기화하고 ij 최단거리와 k를 경유하는 상황의 최단거리를 비교하면 완료되기 때문입니다.
7. 욕심쟁이 알고리즘 1
8. 욕심쟁이 알고리즘 2
본 강의에서는 데이크스트라 알고리즘, 작업 스케줄링, 작업 선택 문제, 허프만 코딩을 살펴봅니다.
8.1 데이크스트라 알고리즘
데이크스트라Dijkstra 알고리즘은 6장의 동적 프로그래밍에서 플로이드Floyd 알고리즘처럼 최단 경로를 구하는 알고리즘입니다. 플로이드 알고리즘은 최적부분구조로 모든 정점 간의 최단 경로를 상향식으로 구하는 방식이고, 데이크스트라 알고리즘은 한 정점으로부터 나머지 모든 정점에 대한 각각의 최단 거리를 구하게 됩니다.
이 알고리즘은 현재 정점에서 인접한 정점까지의 가중치를 이용해 이것을 경유하는 모든 정점까지의 거리를 각각 계산하는데, 이 계산 결과가 기존의 최단 거리보다 작다면 그것으로 갱신하는 방식입니다. 만약 어떤 인접 정점을 경유하여 특정 정점까지 도달하지 못하거나 가중치의 합이 기존의 최단 거리보다 크다면 갱신되지 않겠죠.
특정 정점까지의 최단거리는 보통 d[v] 로 표현하며, 출발점은 자기 자신이므로 최단 거리가 0입니다.
8.2 작업 스케줄링
8.3 작업 선택 문제
8.4 허프만 코딩
Written on March 16th, 2021 by namu